The other day I wrote about my morning session for the summer conference of PCTM (The Pennsylvania Council of Teachers of Mathematics) and today I will write about a session I attended. Unfortunately, child care considerations meant I had to leave at lunch time on Friday but I did have the pleasure of attending a session led by Dr. Daniel Ilaria of West Chester University in Pennsylvania. Professor Ilaria had one of his students, Kaitlin Nora Silard, along with him. She is about to begin her student teaching in the fall. The presentation was titled Learning to Persevere in Problem Solving and its description sort of sang out to me as something that would be of interest to me personally and that might be a great talking point for my department this year. They did not disappoint.
One of the highlights of the discussion – as it should be at a valuable PD event – was the opportunity to share ideas with other educators. There were about a dozen of us in the room and Prof Ilaria was terrific at allowing space for us to discuss and debate. His student Ms Silard was excellent as well. At one point after presenting a problem on the projector Ms Silard walked by and saw I had a solution and I had put my pen down. She looked at my work and simply said ‘Why don’t you try to find another way to solve this?’ Awesome for her and an important reminder for me. I should not let myself get away with a ‘Do what I say, not what I do’ type of attitude. Below is the problem we were working on at the time:
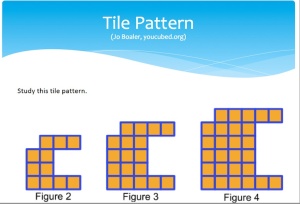
My original approach to this problem is what I would call an additive approach. In figure 2 I saw a row of 3 on top of a rectangle that was 2 by 3 and then 2 left over on the bottom row. In figure 3 I saw a row of 4 on top of a rectangle that was 3 by 4 with 2 left over on the bottom row. In figure 4 I saw a row of 5 on top of a rectangle that was 4 by 5 and then I saw 2 left over on the bottom row. I generalized this as (n+1) + (n(n+1)) + 2 which simplifies as n^2 + 2n + 3
I shared this solution and a number of people shared slightly different – but all additive – solutions, What I mean by this is that all of the techniques of decomposition were rooted in adding up pieces of what we saw. A lovely explanation was presented by Ms Silard that involved moving pieces to simplify a rectangular image. It was great fun working this out and hearing different responses. It was important to both feel good about my solution AND to hear others explain their point of view. It reminded me of Christopher Danielson’s keynote at Twitter Math Camp 2015 (you can view it here and you should, it is fantastic!) When Prof Danielson was speaking about the prompts from his upcoming book and from the great website http://wodb.ca He talked about the importance of having students face a problem that has multiple ‘correct’ answers and developing the ability for them to explain their answers. He also talked about the experience of listening to a different solution and how that can inform your own problem-solving skills. I definitely benefited from listening to the other session participants. But I have to admit that I benefited the most from Ms Silard pushing me to think of another solution. This one was a subtractive solution. I saw a figure that was not really there and then pulled pieces away to create what WAS there. For figure 2 I saw a 4 by 4 square that was missing 5 pieces. For figure 3 I saw a 5 by 5 square that was missing 7 pieces. For figure 4 I saw a 6 by 6 square that was missing 9 pieces. I generalized this as (n + 2)^2 – (2n + 1) and, magically, this turns out to be the same answer. My table mate appreciated this approach more and it was interesting to me that this was the only approach that looked at taking pieces away (pieces that were not really there to begin with) and that this relied on a more stable shape (the n+2 sized square.) The experience of hearing other people’s voices, the experience of thinking of another way to do it myself, and the experience of explaining myself to my table mate and then the whole groups were all powerful experiences. I thank Prof Ilaria and Ms Silard for their careful management of this presentation. I need to revisit these feelings throughout the year and commit myself to trying to create a careful space for my students to experience these powerful feelings as well.
PS – I knew when I read the program for the PCTM conference that Prof Ilaria’s name seemed vaguely familiar. I realized this morning why that is. Back in 2004 I started on a doctoral program at the College of Education at Florida Atlantic University. In 2007, after finishing my course work, I moved away with the intent of finishing my dissertation (titled A Case Study of the Intentions and Actions of Secondary Mathematics Teachers with Regard to Questioning in the Classroom) and an article that Prof Ilaria wrote back in 2002 is in my list of references for my work. Kind of cool to have met him in person now and he was kind enough to share his slide presentation with me via email.